본 포스트는 Ableton사에서 소프트웨어 개발자로 재직 중인 Jack Schaedler님의 DSP 입문 자료 <strong><em>Seeing Circles, Sines And Signals</em></strong> 를 통해 공부하면서 다시 풀어서 정리한 내용입니다.

The Unit Circle : Trigonometry review

unit circle(단위원)과 radian(라디안)

Sine wave와 cosine wave를 설명하는 과정에서 단위원을 따라 회전하는 선의 길이와 움직임을 묘사했었다. 이 단위원의 둘레는 phase(위상)라고 하는데, X축과 회전하는 선이 이루는 각도라고 생각할 수 있다. 아니, 각도를 사용하지 않고 라디안(radians)을 사용하도록 하자.

우리는 원의 둘레를 360도라고 배웠는데, 이번에는 2pi radians(라디안)이라고 불러보자(원의 둘레는 2pi라는 것도 배운 바 있다.) 원을 두 바퀴, 세 바퀴 돌면 720도, 1080도가 되는데 이런 식의 계산은 편리하지가 않다. 두바퀴는 2 * 2pi randians으로 계산하는 것이 더 편하다고 하는데 일단 지켜보자.

아래의 Figure 1.에서처럼 45도의 각도는 45/360 * 2pi = 0.785 radians 로 표현할 수 있다.

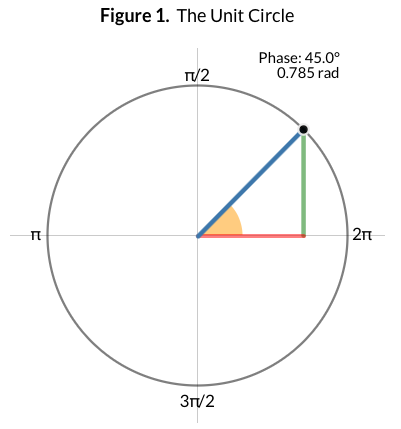
삼각함수 복습

삼각함수를 좀 복습해야겠다. 위의 그림의 삼각형을 보고 다음과 같이 부른다면

• Hypotenuse 빗변 (파랑, 원의 반지름) : r
• Adjacent 밑변 (빨강, x축 길이) : x
• Opposite 높이 (초록, y축 길이) : y

피타고라스의 정리를 통해 다음과 같이 말할 수 있다.

$$x^2 + y^2 = r^2$$

그렇다면, sine, cosine도 다음과 같이 구할 수 있다.

$$\sin = \dfrac{y}{r}$$

$$\cos = \dfrac{x}{r}$$

단위원(unit circle)를 기준으로 본다면 r=1 이므로 다음과 같다.

$$\sin = \dfrac{y}{1}$$

$$\cos = \dfrac{x}{1}$$