추천 시스템의 평가 지표 … ?
추천 시스템은 이름에서도 알 수 있듯, 어떤 사용자가 관심을 가질 법한 아이템을 추천하는 알고리즘이다. 추천 시스템의 성능은 어떻게 평가할 수 있을까? 추천시스템에 대해 깊게 생각하지 않았을 적에는 분류 문제에서 성능을 평가하는 것과 비슷하다고 생각했다. “사용자가 관심을 가질만한 아이템이 맞다 또는 아니다." 를 측정한다면, 우리에게 익숙한 precision, recall 등으로 생각해볼 수도 있을 것 같다.
하지만, 분류 성능 지표에서는 추천의 순서나 순위가 고려되지 않는다. (역시 어줍잖게 생각하면 안 돼 …)
추천 시스템을 통해 추천되는 아이템의 경우 추천의 정도가 동일하지 않다. 대부분의 추천 결과는 다음처럼 나올 수 있다고 생각해 볼 수 있다.
1순위 : 가장 관심을 가질만한 것.
2순위 : 그 다음 차선책으로 관심을 가질만한 것.
3순위 : 그 다음으로 사용자가 관심을 가질만한 것.
4순위 : 또 그 다음 … …
Mean Average Precision (MAP) 은 순서 또는 순위를 감안하는 부분을 반영하여 추천 시스템의 성능을 평가하는 지표로서, 과거 캐글의 Stander Product Recommendation, 카카오아레나의 브런치 사용자를 위한 글 추천 대회 등 추천 시스템 관련 컴퍼티션에서 채점 방식으로 적용되었다. 특히 분류 문제에서 흔히 언급되는 Precision과 Recall이 적용된 성능평가 방법으로, 아주 낯설지는 않다.
Precision & Recall
| Predict Positive | Predict Negative | |
|---|---|---|
| Actual Positive | True Positive | False Negative |
| Actual Negetave | False Positive | True Negative |
MAP에 대한 개념는 Precision과 Recall에서부터 시작한다. 일반적으로 위와과 같이 confusion matrix가 있다고 할 때, Precision과 Recall은 다음과 같다. (더 자세한 설명은 링크를 참조하도록 하자)
$$\text{Precision} = \frac{\text{True Positive}}{\text{True Positive + False Positive}}$$
$$\text{Recall} = \frac{\text{True Positive}}{\text{True Positive + False Negative}}$$
추천시스템 관점에서의 Precision & Recall
추천시스템에서는 Precision과 Recall을 다음과 같이 해석할 수 있다. 추천시스템에서는 분자 부분을 relevant(관련있는) 라고 표현하기도 한다.
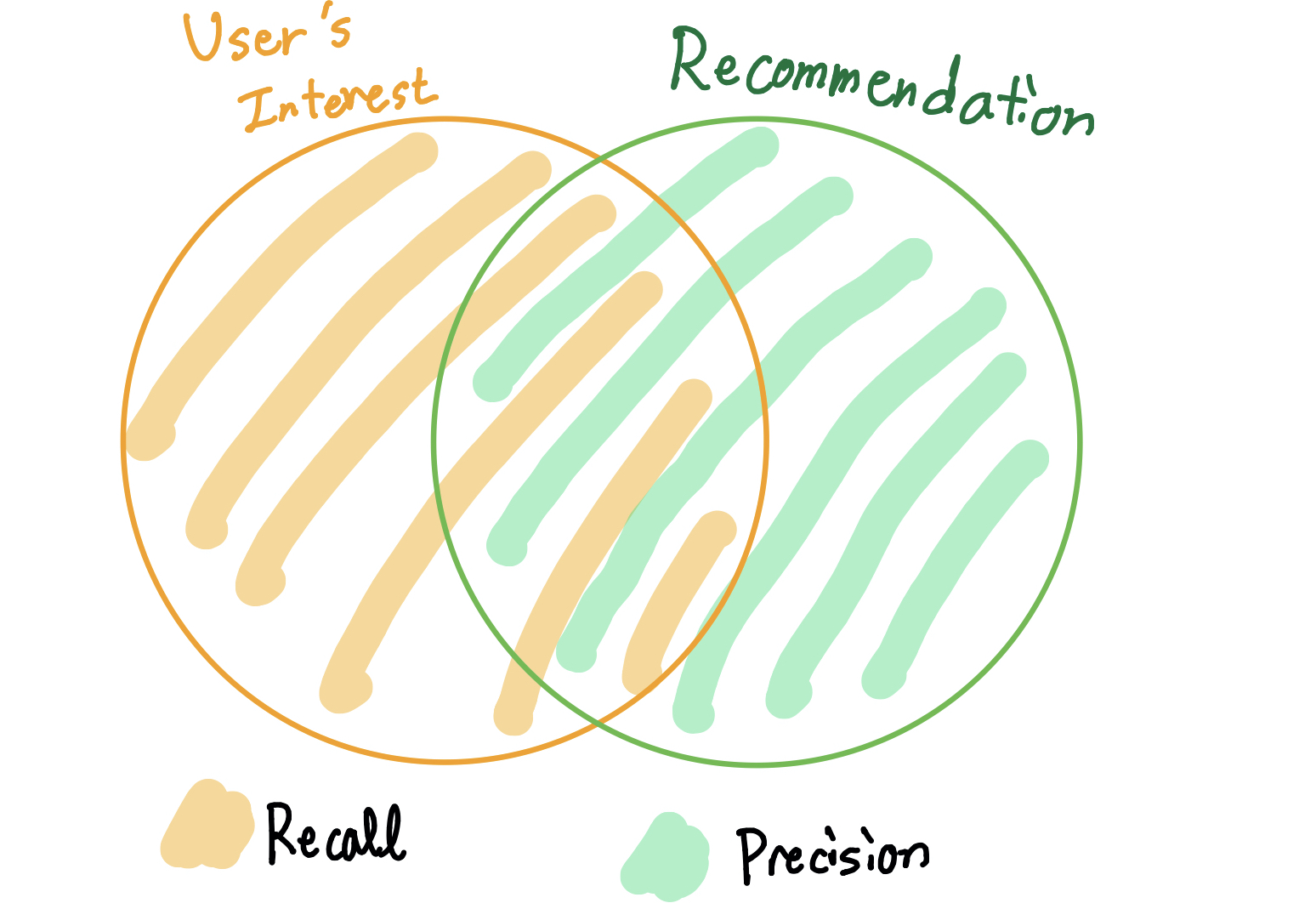
Precision 또는 \(P\):
- 추천한 아이템 중, 실제로 사용자의 관심사와 겹치는 아이템의 비율
- \(\text{Precision} = \frac{\text{Items from recommendation that fit user’s interest}}{\text{Total items from recommendation}}\)
Recall 또는 \(r\):
- 실제로 사용자가 관심을 가진 아이템 중, 추천된 아이템이 겹치는 비율
- \(\text{Recall} = \frac{\text{Items from recommendation that fit user’s interest}}{\text{User’s interest}}\)
Cutoff (@K)
MAP에서는 Cutoff의 개념이 등장한다. Cutoff는 “잘라낸다"는 뜻으로, 쉽게 말하면 “상위 K개만 고려하고 그 아래로는 쳐내기” 라고 이해하면 된다. Cutoff를 가질 경우에는, @K 를 덧붙여서 표기한다.
어떠한 사용자의 기록을 통해서 자동차 용품와 관련된 아이템을 추천한 결과가 다음과 같다고 하자.
| 순위 | 추천 아이템 | 정답 / 오답 |
|---|---|---|
| 1 | 엔진 오일 | 정답 |
| 2 | 자동차 배터리 | 정답 |
| 3 | 차량용 방향제 | 정답 |
| 4 | 자동차 장난감 | 오답 |
| 5 | 자동차 워셔액 | 정답 |
| 6 | 초보운전 스티커 | 오답 |
| 7 | 타이어 | 정답 |
| 8 | 운전자 보험 상품 | 오답 |
| 9 | 렌트카 이용권 | 오답 |
| 10 | 자동차 핸드폰 거치대 | 정답 |
다음 예시의 추천시스템의 결과에 대하여 \(k\)개 Cutoff를 적용하여 Precision을 구한다면, 이를 Precision@K라고 한다. Precision@K는 Cutoff에 따라 달라질 수 있다.
- Cutoff k=10인 경우 \(\rightarrow P(k=10) = 0.6\)
| 순위 | 추천 아이템 | 정답 / 오답 |
|---|---|---|
| 1 | 엔진 오일 | 정답 |
| 2 | 자동차 배터리 | 정답 |
| 3 | 차량용 방향제 | 정답 |
| 4 | 자동차 장난감 | 오답 |
| 5 | 자동차 워셔액 | 정답 |
| 6 | 초보운전 스티커 | 오답 |
| 7 | 타이어 | 정답 |
| 8 | 자동차 보험 상품 | 오답 |
| 9 | 렌트카 이용권 | 오답 |
| 10 | 자동차 핸드폰 거치대 | 정답 |
- Cutoff k=3인 경우 \(\rightarrow P(k=3) = 1\)
| 순위 | 추천 아이템 | 정답 / 오답 |
|---|---|---|
| 1 | 엔진 오일 | 정답 |
| 2 | 자동차 배터리 | 정답 |
| 3 | 차량용 방향제 | 정답 |
- Cutoff k=5인 경우 \(\rightarrow P(k=5) = 0.8\)
| 순위 | 추천 아이템 | 정답 / 오답 |
|---|---|---|
| 1 | 엔진 오일 | 정답 |
| 2 | 자동차 배터리 | 정답 |
| 3 | 차량용 방향제 | 정답 |
| 4 | 자동차 장난감 | 오답 |
| 5 | 자동차 워셔액 | 정답 |
- Cutoff k=7인 경우 \(\rightarrow P(k=7) = 0.714\)
| 순위 | 추천 아이템 | 정답 / 오답 |
|---|---|---|
| 1 | 엔진 오일 | 정답 |
| 2 | 자동차 배터리 | 정답 |
| 3 | 차량용 방향제 | 정답 |
| 4 | 자동차 장난감 | 오답 |
| 5 | 자동차 워셔액 | 정답 |
| 6 | 초보운전 스티커 | 오답 |
| 7 | 타이어 | 정답 |
Average Precision (AP@K)
Cutoff가 \(K\)개인 Average Precision(AP@K)은 Precision@K의 평균을 구하는 과정이다.
$$ AP@K = \frac{1}{m} \sum_{j=1}^K P(j) \cdot rel(j) \dots \begin{cases} rel(j)=1 & \text{if } j^{th} \text{ item is relevant}, \cr rel(j)=0 & \text{if } j^{th} \text{ item is not relevant}, \cr \end{cases} $$
- \(K\) : Cutoff 갯수
- \(m\) : 추천 아이템 중 relevance가 있는 아이템의 갯수 (number of relevant document)
- \(j\) : 전체 추천 아이템 리스트 중, 해당 추천 아이템의 index
- \(P(j)\) : \(j\)번째 까지의 precision값
- \(rel(j)\) : \(j\)번째의 relevance 여부
위에서 예시로 들었던 자동차용품 추천결과를 통해, [\(AP@5\), \(AP@7\), \(AP@9\), \(AP@10\)] 을 계산해 보았다. 특히 \(AP@7\) 와 \(AP@9\) 의 결과에서 관찰할 수 있듯이, \(\frac{1}{m}\)에서 \(m\)은 relevance가 있는 경우만을 포함하기 때문에, 뒤에서 오답이 추가되어도 AP의 값이 페널티를 받지는 않는다.
$$AP@5 = \frac{1}{4} \cdot \left(\frac{1}{1} + \frac{2}{2} + \frac{3}{3} + 0 + \frac{4}{5}\right) = 0.95$$
$$AP@7 = \frac{1}{5} \cdot \left(\frac{1}{1} + \frac{2}{2} + \frac{3}{3} + 0 + \frac{4}{5} + 0 + \frac{5}{7} \right) = 0.90$$
$$AP@9 = \frac{1}{5} \cdot \left(\frac{1}{1} + \frac{2}{2} + \frac{3}{3} + 0 + \frac{4}{5} + 0 + \frac{5}{7} + 0 + 0 \right) = 0.90$$
$$AP@10 = \frac{1}{6} \cdot \left(\frac{1}{1} + \frac{2}{2} + \frac{3}{3} + 0 + \frac{4}{5} + 0 + \frac{5}{7} + 0 + 0 + \frac{6}{10}\right) = 0.85$$
또한, 아래의 예시에서 Case A와 Case B를 비교해보면, 순위가 높은 추천 아이템이 정확할 수록 높은 AP값이 계산되므로, 추천의 순서 또는 순위가 평가 지표에 영향을 끼침을 알 수 있다.
$$AP@5 = \frac{1}{3} \cdot \left(\frac{1}{1} + 0 + \frac{2}{3} + 0 + \frac{3}{5}\right) = 0.75 \dots \text{(Case A)}$$
$$AP@5 = \frac{1}{3} \cdot \left(0 + \frac{1}{2} + 0 + \frac{2}{4} +\frac{3}{5} \right) = 0.53 \dots \text{(Case B)}$$
Mean Average Precision (MAP@K)
AP는 각각의 사용자(또는 쿼리)에 대하여 계산한 것이므로, 각 사용자에 따라 AP값이 산출된다. Mean Average Precision(MAP)은 AP값들의 Mean을 구한 것으로, 식은 다음과 같다.
$$MAP@K = \frac{1}{U} \sum_{u=1}^{U} (AP@K)_u$$
- \(U\) : 총 사용자의 수
마무리하며
이번 MAP에 대해 알아보았다. 다음 포스트에서는 역시나 추천시스템의 평가지표로 자주 등장하는 DCG(Discounted Cumulative Gain)에 대해서 공부하고 정리 할 예정이다.
AP, MAP의 파이썬 코드로 된 구현체는 링크를 통해 참조할 수 있다.