본 포스트는 Ableton사에서 소프트웨어 개발자로 재직 중인 Jack Schaedler님의 DSP 입문 자료 <strong><em>Seeing Circles, Sines And Signals</em></strong>를 통해 공부하면서 다시 풀어서 정리한 내용입니다.
The Wagon Wheel Effect
빠르게 회전하는 바퀴나 물체를 보면 처음에는 반시계 방향으로 회전하는가 싶더니, 어느 순간부터 반대로 시계방향으로 회전하는 것 같은 환영을 볼 수 있다. 아니면 분명히 바퀴는 빠르게 회전하는데, 느리게 회전하는 것처럼 보일 때도 있다. 바로 undersampling과 alias 로 인해 발생하는 현상인데, 명칭은 Wagon Wheel Effect(마차바퀴현상)라 한다. (영상)
원본의 Figure. The Wagon Wheel Effect에서 하단의 sampling rate 슬라이더를 조절하며 왼쪽의 시계방향으로 회전하는 물체와, 오른쪽의 sampling rate에 따른 스냅샷(혹은 샘플)를 관찰해보자
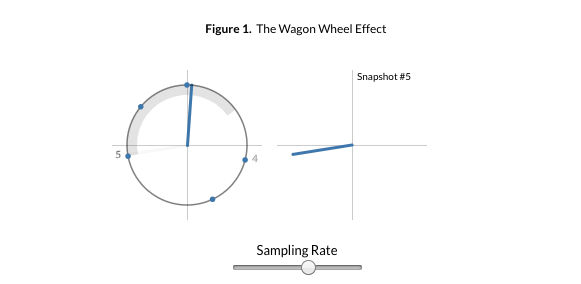
직관적으로 봤을 때, 왼쪽과 마찬가지로 오른쪽 스냅샷도 시계방향으로 회전하는 듯한 모션을 취하기 위해서는 최소한 왼쪽에서 한번 회전하는 동안 2번 이상의 스냅샷을 찍어야 한다. 만약 sampling rate을 엄청 낮게 설정한다면 스냅샷은 기존의 회전 방향과는 반대로 반시계 방향으로 찍히게 된다.
회전 방향이 결정되지 않고 정지해 있는 듯한 특이한 케이스도 있다. 만약 sampling rate을 한바퀴당 1번으로 설정한다면 스냅샷에는 움직임이 없을 것이고, sampling rate을 한바퀴당 2번으로 설정한다면 스냅샷은 그냥 앞뒤로만 움직이기 때문에 진행 방향을 유추할 수 없게 될 것이다.
Sine Wave Aliasing : Multiples of the sampling rate
Sive wave에는 다음과 같은 법칙이 있다.
sampling rate이 \(SR\) 헤르쯔와 정수 \(K\)가 주어졌을 때,
\(F\) 라는 frequency를 지닌 sine wave가 있고, \(F+(k * SR)\) 의 진동수를 지닌 sine wave를 샘플링했다고 할 때, 둘은 서로 구별이 가능하지 않다.
예를 들어, Sampling rate이 6Hz라고 했을 때, 다음 두 그룹의 sive wave는 서로 구별이 가능하지 않다.
- 샘플링을 거친 1Hz의 sine wave
- 샘플링을 거친 다음 세 가지의 sine wave
- \( 1+(1 * 6) = 7Hz \)
- \( 1+ (2 * 6) = 13Hz \)
- \( 1+(3 * 6) = 19Hz \)
(사실 여기까지는 조금 이해가 안 갔는데 …)
원본의 Figure. All Sampled Sine Waves Have Aliases을 보면 더욱 직관적이다. Figure 1.의 Time domain 그래프는 1Hz sine wave(파랑색)와, 그 외 sine wave(회색)을 비교하고 있다. 샘플링을 거치고 나면(Frequency domain 그래프), 샘플링이 표현하는 부분은 파랑색과 회색 다 일치하기 때문에, 샘플링을 한 뒤에는 각각 어떤 frequency 였는지 구분을 할 수 가 없게 된다.
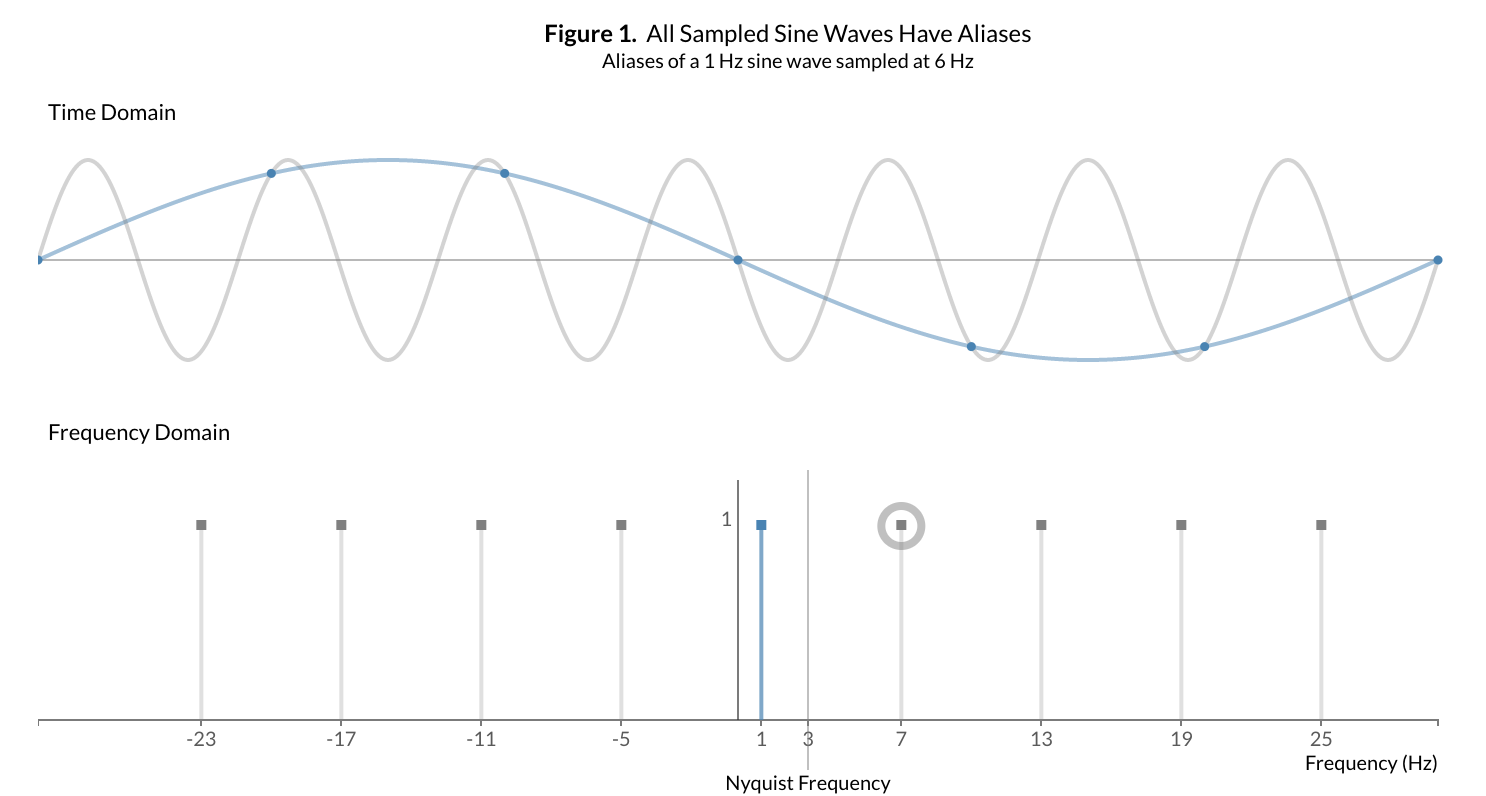
이 말인즉슨, 샘플링을 거친 sine wave는 무한대의 alias를 가진다는 것이다. 그저 기존의 frequency에 sampling rate의 배수만 더해주면 기존 frequency에 대한 새로운 alias가 형성된다. 따라서 이 법칙은, 어떠한 신호라도 샘플링을 거치면 다른 샘플링 신호와 구별이 가능하지 않는 상황이 올 수 있다는 것을 의미한다.