1. 소리 데이터란

소리는 다음 과정에서 생산된 것을 의미합니다.

• (1) 어떠한 물체 또는 매질(object)의 진동(vibration)으로 인해 공기 입자들이 밀고 당겨지는 반복적인 과정(oscilation)에서 생긴 파동(wave)
• (2) 공기의 압력이 낮아지면 빈 공간이 생기면서 다른 입자들로 채워지고, 압력이 높아지만 입자들을 밀어내는, 밀고 당기는 반복적인 연쇄 작용(oscillation)으로 인해 생기는 파동(wave)

그리고 위에서 정의한 파동은 아래와 같은 파형(waveform)으로 나타낼 수 있습니다.

2. 소리 데이터의 표현

2.1. 파형의 요소

파형을 통해서 우리는 다음과 같은 정보를 파악할 수 있습니다. 주로 파동을 표현하는 요소들이죠.

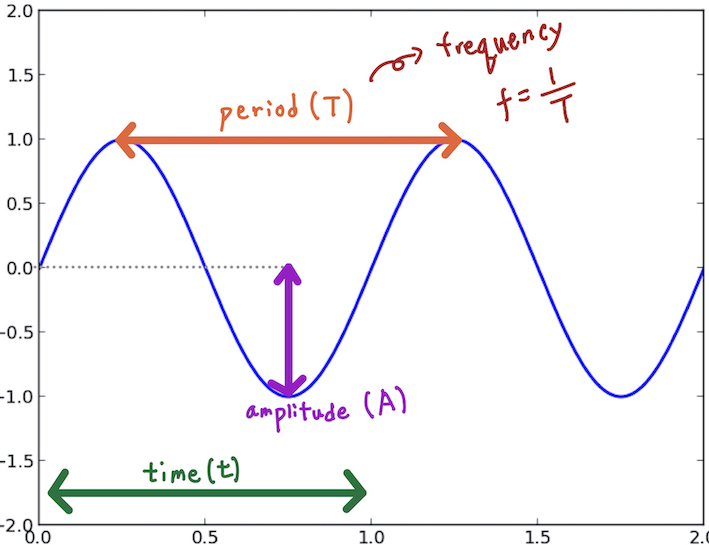
• 시간(time): 파동이 진행되는 시간. 주로 X축입니다.
• 진폭(amplitude): 진동의 중심에서 최대까지의 거리를 나타냅니다. 진동의 크기를 의미하고, $A$라고 나타냅니다.
• 주기(period): 1회 진동하는데 걸리는 시간입니다. \(T\) 라고 나타냅니다.
• 진동수(또는 주파수. frequency): 한 점이 1초동안 진동한 횟수. \(f\) 라고 나타냅니다.
  • 주기와 진동수는 서로 역수인 관계를 보입니다. (\(f = \frac{1}{T}\) 또는 \(T = \frac{1}{f}\))
  • 따라서, 주기가 길수록 진동수는 작고 주기가 짧을 수록 진동수는 큰 관계를 보입니다.

2.2. 파형의 수학적 표현

파형은 사인함수를 통해 다음과 같이 수학적으로도 표현할 수 있습니다.

\(y(t) = A \sin(2 \pi f t + \phi)\)

• \(A\) : 진폭(amplitude)
• \(sin\) : 사인함수
• \(f\) : 진동수(frequency)
• \(t\) : 시간(time)
• \(\phi\) : 위상(phase). 위상이란 진동체의 상대적인 위치변화를 나타내는 부분입니다. 위상값에 따라 파형이 왼쪽으로 또는 오른쪽으로 이동(shift)된 형상인지를 알 수 있습니다.

2.3. 진폭, 진동수의 관계

진동과 진폭이 소리와 무슨 관계가 있는지 아직 많이 낯선데요. 우선 진동 수와 음의 높낮이(pitch)의 관계에 대해 알아보겠습니다. 진동수가 클 수록 음이 높아집니다. 즉, 진동한 횟수가 많을 수록 높은 음이 구현된다고 이해할 수 있습니다. 반대로 진동한 횟수가 적다면, 그만큼 음의 높이가 낮은 저음이 구현됩니다. 아래와 같이 정리해볼 수 있습니다.

• frequency \(\leftrightarrow\) pitch
  • longer periods(\(T\)) \(\rightarrow\) lower frequency(\(f\)) \(\rightarrow\) lower pitch
  • shorter periods(\(T\)) \(\rightarrow\) higher frequency(\(f\)) \(\rightarrow\) higher pitch

이번에는 진폭과 소리의 크기(loudness)의 관계에 대해 알아보겠습니다. 진폭이 클 수록 소리는 크고, 진폭이 작을 수록 소리도 작아집니다. 아래와 같이 정리해볼 수 있습니다.

• amplitude \(\leftrightarrow\) loudness
  • larger amplitude(\(A\)) \(\rightarrow\) louder
  • smaller amplitude(\(A\)) \(\rightarrow\) quietter

3. ADC (Analog digital conversion)

우리가 듣는 소리 그 자체, 즉 아날로그 소리는 연속적(continuous)입니다. 따라서 소리를 분석하기 위해서는 아날로그 소리를 디지털적인 형태로 변환하는 작업을 거쳐야 하는데 이를 Analog digital conversion(ADC)이라고 합니다. 말 그대로 아날로그를 디지털로 변환하는 작업이죠.

3.1. Sampling & Quantization

ADC에는 샘플링(Sampling)과 양자화(Quantization)이라는 두 가지 과정을 통해 연속적인 아날로그 소리를 이산적인 데이터로 변환합니다.

• Sampling: 샘플링은 시간의 흐름에 따라 진행되는 연속적인 신호를 특정 주기(time intervial)에 맞추어 신호를 이산적인 시간으로 쪼개는 과정입니다.
• Quantization: 양자화는 샘플링되어 저장된 데이터를 연속적이지 않은 대표값으로 정수화하여 이산적인 값으로 변환합니다.

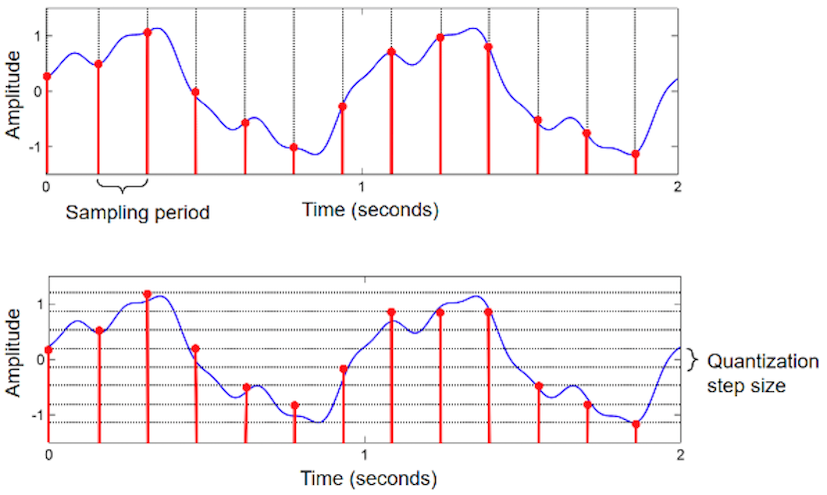
3.2. Sample rate & Bit depth

샘플링과 양자화는 적용되는 방법에 따라, 변환된 데이터의 품질에 영향을 끼칠 수 있습니다. 예를 들어 샘플링 주기나 양자화가 너무 크게 적용된다면, 기존의 아날로그 소리가 지닌 세세한 정보가 손실될 수도 있습니다. 이러한 품질을 결정하는 기준에는 샘플링주기(Samplig rate)과 비트뎁스(Bit depth)가 있습니다.

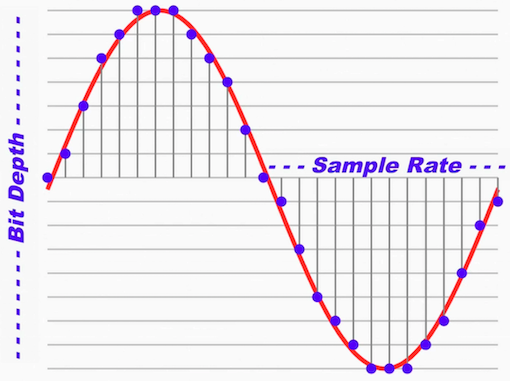
• Sampling rate: 1초 동안 담긴 샘플의 개수. 샘플링주기가 높을 수록 시간의 흐름에 따른 신호의 손실이 적습니다.
• Bit depth: 진폭을 쪼개는 개수. 비트(bit) 개수가 클 수록 기존의 신호에 유사한 형태로 데이터를 저장할 수 있습니다.

4. 세줄 … 아니 쓰다 보니 다섯줄 요약

우리가 귀로 듣는 소리에 대한 간단한 정의와, 소리를 분석하기 위해 디지털적인 정보로 변환하는 작업에 대해 알아보았습니다.

• 소리는 공기의 진동(vibration)과 반복적인 움직임(oscillation)으로 인해 압력이 변화하면서 생긴 파형이며 연속적인 아날로그 신호이다.
• 아날로그 소리를 분석하기 위해서는 ADC를 통해 디지털적이고 이산적인 데이터로 변환한다.
• 샘플링(sampling)은 아날로그 소리의 시간흐름을 특정 주기로 쪼개어 변환하는 작업이며, 샘플링주기(sampling rate)에 따라 1초 동안 기록되는 샘플의 개수를 달리할 수 있다.
• 양자화(quantization)는 아날로그 소리의 크기를 특정 구간으로 쪼개어 변환하는 작업이며, 비트뎁스(bit depth)에 따라 그 구간의 세밀함을 조절할 수 있다.
• 샘플링 주기와 비트뎁스는 아날로그 소리를 디지털 데이터로 변환되는 품질을 결정하며, 세밀할 수록 정보의 손실을 줄이고 기존의 소리에 유사한 데이터를 기록할 수 있다.

다음 포스트에서는 파형을 분석하기 위해 사용되는 푸리에 변환 (Fourier Transform)에 대해서 정리해보도록 하겠습니다.