0. 데이터와 librosa
실제로 소리 데이터를 다뤄보기 위해서 음악 데이터를 준비하겠습니다. 음악 장르 분류 데이터셋으로 유명한 GTZAN Dataset을 다운받아 음악 파일을 하나 선택했습니다.
그리고 Librosa는 오디오와 음악 분석을 위 빠질 수 없는 파이썬 패키지입니다. 음원이나 소리 파일을 불러와 waveform을 시각화 하거나 다른 형태로 변환할 수 있는 기능을 제공합니다.
( Librosa는 pip install librosa 명령어를 통해 설치할 수 있습니다. )
import warnings
warnings.filterwarnings(action='ignore')
import numpy as np
import matplotlib.pyplot as plt
import IPython.display as ipd
import librosa
import librosa.display
file_path = 'disco.00054.wav' # 실습에 사용할 음악 파일
어떤 음악인지 한번 들어볼까요?
ipd.Audio(file_path)
1. Waveform
음원을 아래처럼 간단하게 읽어와보겠습니다. 튜플인 결과값에서 첫 번째는 numpy array형태의 waveform의 amplitude값이고, 두 번째 값은 sampling rate으로, 초당 샘플 갯수를 의미합니다. Sampling rate는 파일을 읽을 때, parameter로 설정할 수 있습니다. Default값은 22050입니다.
wav, sr = librosa.load(file_path)
print("Amplitude: \n", wav)
print("Sampling rate: ", sr)
Amplitude:
[-0.08001709 -0.07550049 -0.08358765 ... 0.08270264 0.10083008
0.10562134]
Sampling rate: 22050
시각화를 통해 데이터가 아래와 같은 형태의 waveform을 띄고 있음을 확인해 볼 수 있습니다.
fig = plt.figure(figsize = (14,5))
librosa.display.waveplot(wav, sr=sr)
plt.ylabel("Amplitude")
plt.show()
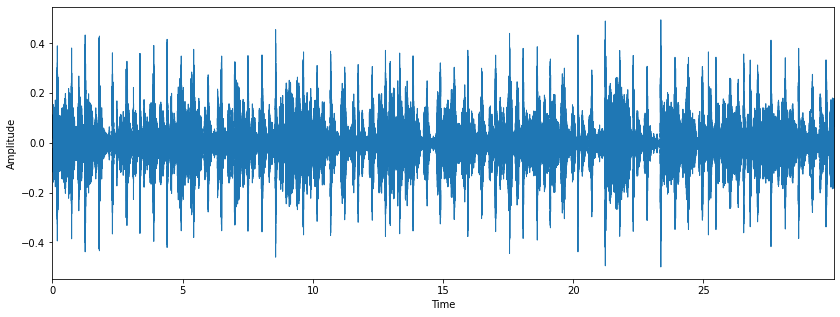
2. FFT (Fast Fourier Transform)
앞서 다룬 포스트에서 time-domain의 waveform을 FFT(Fast Fourier Transform)을 통해 분해(decompose)하고, frequency-domain으로 변환하여 원본 소리 데이터를 형성하는 주파수(frequency)의 정도를 파악하고 시각화 할 수 있다고 이해했습니다. 이번에는 numpy를 통해 앞서 구한 waveform amplitude에 FFT를 적용할 수 있습니다.
FFT를 적용하여 시각화한 결과는 아래와 같습니다. 주로 1000Hz 이하로 많이 분포해 있는 것을 확인할 수 있네요.
fft = np.fft.fft(wav)
magnitude = np.abs(fft)
frequency = np.linspace(0, sr, len(magnitude))
left_frequency = frequency[:int(len(frequency)/2)]
left_magnitude = magnitude[:int(len(magnitude)/2)]
fig = plt.figure(figsize = (14,5))
plt.plot(left_frequency, left_magnitude)
plt.xlabel("Frequency")
plt.ylabel("Magnitude")
plt.show()
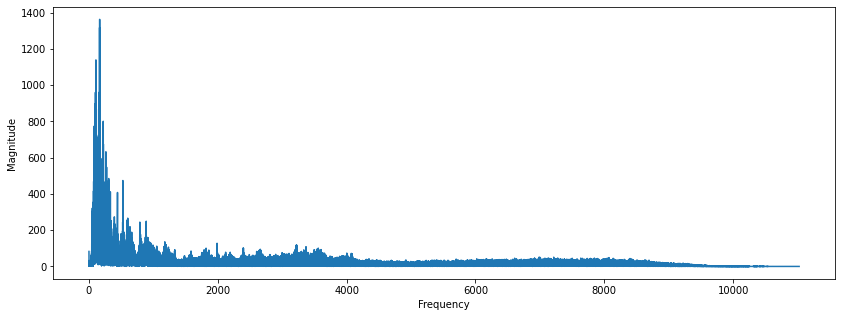
3. STFT (Short-Time Fourier Transform)
STFT(Short-Time Fourier Transform)은 시간 정보가 유실되는 것을 방지하기 위해, 사전에 정의한 시간의 간격(window 또는 frame) 단위로 쪼개어 푸리에 변환을 적용하는 기법입니다. STFT는 librosa를 통해 적용할 수 있습니다. 이때, window의 크기(n_fft)와 window 간에 겹치는 사이즈(hop_length)를 설정해줍니다. 일반적으로는 n_fft의 1/4 정도가 겹치도록 설정한다고 합니다.
n_fft = 2048
hop_length = 512
stft = librosa.stft(wav, n_fft = n_fft, hop_length = hop_length)
spectrogram = np.abs(stft)
print("Spectogram :\n", spectrogram)
Spectogram :
[[1.42030740e+00 7.47260690e-01 5.37097007e-02 ... 1.88164175e-01
1.21684396e+00 2.43966293e+00]
[1.24079692e+00 6.81115210e-01 6.51928782e-02 ... 2.08189130e-01
1.22743416e+00 2.52433753e+00]
[1.09137118e+00 4.82469022e-01 1.85490116e-01 ... 6.99194148e-02
1.43492615e+00 2.53518319e+00]
...
[3.84226470e-04 1.63909295e-04 9.80101977e-05 ... 2.23124225e-04
2.80503096e-04 1.98973445e-04]
[3.00532440e-04 1.77996873e-04 1.29194887e-04 ... 9.72686321e-05
2.01086092e-04 9.30428141e-05]
[2.59254826e-04 9.42422412e-05 5.96536411e-05 ... 7.49909232e-05
1.41018099e-04 1.10232315e-04]]
3.1. Spectogram
STFT를 적용하여 구한 spectogram을 아래와 같이 시각화 해봤습니다. x축은 시간, y축은 주파수, 그리고 주파수의 정도를 색깔로 확인할 수 있습니다. 그런데 값이 너무 미세해서 차이를 파악하고 관찰하기 적합하지 않습니다.
fig = plt.figure(figsize = (14,5))
librosa.display.specshow(spectrogram, sr=sr, hop_length=hop_length)
plt.xlabel("Time")
plt.ylabel("Frequency")
plt.plasma()
plt.show()
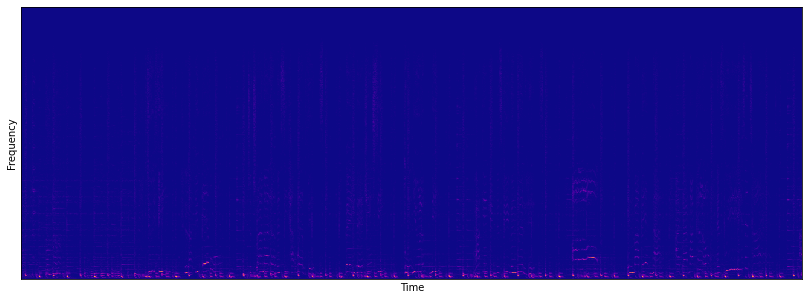
3.2. Log-spectogram
그래서 보통 푸리에변환 이후 dB(데시벨) scaling을 적용한 Log-spectogram을 구합니다. 다분히 시각적인 이유뿐만 아니라, 사람의 청각 또한 소리를 dB scale 로 인식하기 때문에, 이를 반영하여 spectogram을 나타내는 것이 분석에 용이합니다.
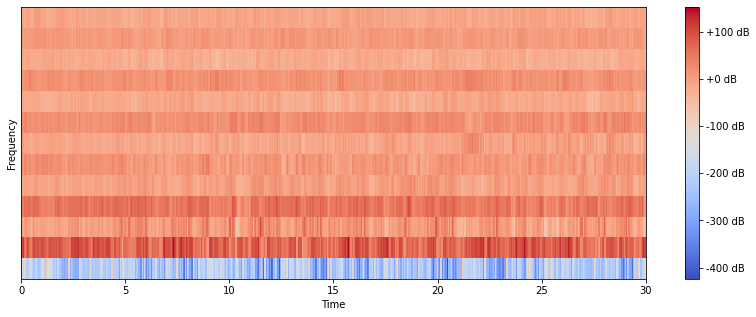
librosa.amplitude_to_db()를 통해 Log-spectogram을 구하여 시각화 한 결과입니다. 대부분의 에너지가 1024Hz이하의 낮은 주파수대역에 모여 있는 것을 볼 수 있네요.
log_spectrogram = librosa.amplitude_to_db(spectrogram)
fig = plt.figure(figsize = (14,5))
librosa.display.specshow(log_spectrogram,
sr=sr,
hop_length=hop_length,
x_axis='time',
y_axis='log')
plt.xlabel("Time")
plt.ylabel("Frequency")
plt.colorbar(format='%+2.0f dB')
plt.show()
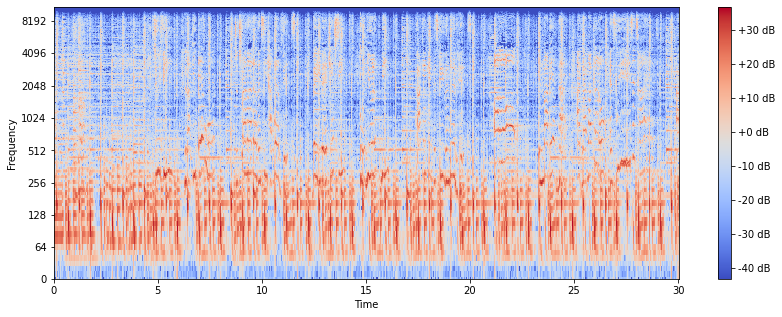
4. MFCC
마지막으로 MFCC(Mel Frequency Cepstral Coefficient)를 구하고 시각화해보겠습니다. MFCC는 오디오 신호 처리 분야에서 많이 사용되는 소리 데이터의 특징값(Feature)으로, 사람의 청각이 예민하게 반응하는 정보를 강조하여 소리가 가지는 고유한 특징을 추출한 값입니다.
마찬가지로 librosa.feature.mfcc()를 통해 feature값을 아래와 같이 추출할 수 있습니다. 파라미터 중 n_mfcc는 추출하고자 하는 mfcc의 개수입니다. 이번 실습에서는 13개로 설정했습니다.
MFCCs = librosa.feature.mfcc(wav,
sr = 22050,
n_fft = n_fft,
hop_length = hop_length,
n_mfcc = 13) # number of coefficient we want to extract
print("MFCCs Shape: ", MFCCs.shape)
print("MFCCs: \n", MFCCs)
MFCCs Shape: (13, 1293)
MFCCs:
[[-176.91516 -173.07141 -171.01598 ... -144.9992 -153.77185
-155.61522 ]
[ 118.94415 117.39079 108.01162 ... 111.50748 108.44453
113.359665 ]
[ -12.249197 -16.364796 -20.116379 ... -68.0366 -40.615326
-32.124104 ]
...
[ -7.0000467 -8.825797 -10.732431 ... -16.528994 -17.69807
-21.954914 ]
[ 10.861979 10.393564 7.8947186 ... -8.206779 -3.6493917
-4.4267316]
[ -12.490692 -10.728968 -14.610505 ... -2.9667187 -12.053108
-9.9868355]]
fig = plt.figure(figsize = (14,5))
librosa.display.specshow(MFCCs,
sr=sr,
hop_length=hop_length,
x_axis='time',)
plt.xlabel("Time")
plt.ylabel("Frequency")
plt.colorbar(format='%+2.0f dB')
plt.show()
5. 한줄 요약
- Librosa라는
킹갓제너럴파이썬 패키지를 이용해서 소리 데이터를 불러오고, 변형할 수 있다!