애매모호하게만 알고 있는 자료구조를 다시 공부하고 정리하는 포스트입니다. 잘 못 이해하고 있는 부분이 있다면 주저없이 지적 부탁 드립니다 :)

1. 알고리즘 복잡도

1.1. 개념

1.1.1. 알고리즘 복잡도 계산이 필요한 이유

• 하나의 문제를 푸는 방법(알고리즘)은 다양할 수 있음.
• 여러가지 방법 중 어느 방법이 더 좋은지를 분석하기 위해 복잡도를 정의하고 계산함.
• 어느 것이 더 좋은 알고리즘인지 판단하는 기준이 됨.

1.1.2. 알고리즘 복잡도를 계산하는 방식

1. 공간 복잡도 (space complexity)
   • 알고리즘이 사용하는 메모리 사이즈
2. 시간 복잡도 (time complexity)
   • 알고리즘 실행 속도
   • 특히, 시간 복잡도에 대한 이해는 필수

1.1.3. 알고리즘 시간 복잡도의 주요 요소

• 반복문이 얼마나 시행되었는지에 따라 시간 복잡도의 성능이 결정된다고 할 수 있음.
• 입력의 크기가 커지면 커질 수록 반복문이 알고리즘 수행 시간을 지배함.

1.2. 복잡도 표기법 유형

1.2.1. Big-O 표기법 \(O(N) \)

• 알고리즘 최악의 실행시간을 표기함
• 아무리 최악의 상황이라도 이 정도의 성능은 보장한다는 의미
• 가장 많이(일반적으로) 사용함

1.2.2. 오메가 표기법 \(\Omega(N) \)

• 최상의 알고리즘 실행 시간을 표기

1.2.3. 세타 표기법 \(\Theta(N) \)

• 알고리즘 평균 실행 시간을 표기

1.3. Big-O 표기법

1.3.1. \( O(n) \)

• 입력 \(n \)에 따라 결정되는 시간 복잡도 함수.
  • \(O(1) \)
  • \(O(\log n) \)
  • \(O(n) \)
  • \(O(n \log n) \)
  • \(O(n^2) \)
  • \(O(2^n) \)
  • \(O(n!) \)
• 입력에 따라 기하급수적으로 시간 복잡도가 늘어날 수 있음.
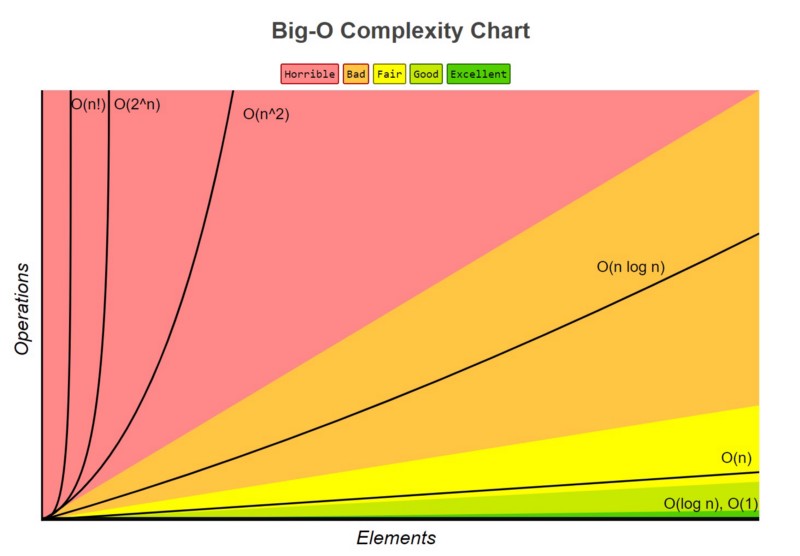
  • \(O(1) < O(\log n) < O(n) < O(n \log n) < O(n^2) < O(2^n) < O(n!) \)

1.3.2. 계산법

• \(O(1) \)
  • 단순하게 입력 \(n \)에 따라 멸번 실행이 되는지 계산함.
  • 실행은 무조건 2회(또는 상수회) 실행한다.

      if n > 10:
          print(n)
  

• \(O(n) \)
  • \(n \)에 따라 \(n \)번 또는 \(k \cdot n + b \) 실행한다.

      for idx in range(n):
          print(idx)
  

• \(O(n^2) \)
  • \(n \)에 따라 \(n^2 \)번 또는 \(k \cdot n^2 + b \) 등을 실행한다.

      for num in range(n):
          for index in range(n):
                  print(index)
  

1.3.3. 표기 방법

• 시간복잡도는 결국 입력값 \(n \)에 따라 성능이 결정됨.
• 결국 알고리즘 성능에 가장 영향을 끼치는 값을 기준으로 표기함.
• 따라서 상수 \(k, b \)는 표기할 때 생략함
• \(k \cdot n^2 + b \)의 경우 Big-O 표기법으로는 \(O(n^2) \)으로 표기함.

2. Reference

• Fastcampus 알고리즘 / 기술면접 강의