1. 트리의 개념
1.1. 트리의 정의
- 노드와 브랜치를 활용하여 구성한 데이터 구조
1.2. 트리와 관련된 용어

트리 관련 용어
- 노드(Node)
- 데이터를 저장하는 기본 요소
- 다른 노드와 연결되는 브랜치에 대한 정보도 포함
- 브랜치(Branch)
- 상위 노드와 하위 노드를 연결하는 가지
- 루트노드(Root Node)
- 트리 최상단에 위치한 최상위 노드
- 레벨(Level)
- 최상위 노드를 Level 0이라고 할 때, 특정 레벨에 위치한 노드의 집합
- 부모 노드(Parent Node)
- 상위 노드
- 자식 노드(Child Node)
- 하위 노드
- 단말 노드(Leaf Node)
- 하위 노드가 없는 노드
- 형제 노드(Sibling Node)
- 동일한 부모 노드를 가진 노드
- 깊이(Depth)
- 루트에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수
- 크기(Size)
- 자신을 포함한 모든 자식노드의 개수
- 높이(Height)
- 하위 트리 개수 / 간선 수 (degree) = 각 노드가 지닌 가지의 수
- 노드의 차수(Degree of Node)
- 각 노드가 지닌 가지의 수
- 트리의 차수(Degree of Tree)
- 트리의 최대 차수
트리의 종류
- 이진 트리 vs 이진 탐색 트리
- 이진 트리(Binary Tree)
- 노드의 최대 브랜치가 2개인 트리
- 이진 탐색 트리(Binary Search Tree: BST)
- 왼쪽 노드는 해당 노드보다 작은 값, 오른쪽 노드는 해당 노드보다 큰 값을 가지는 조건이 적용된 이진트리
- 이진 트리(Binary Tree)
1.3. 트리의 적용 예시
- 주요 용도: 데이터 검색(탐색)
1.4. 이진 탐색 트리의 시간복잡도
- 트리의 높이(Depth)를 \(h\)라고 표기한다면, 시간복잡도는 \(O(h)\)
- 노드의 개수가 \(n\)일 때,
- 트리의 높이 \(h = \log_2n\) 에 가까움. 시간 복잡도는 \(O(\log n)\) -> (빅오 표기법에서 \(\log\)의 밑은 2)
- 한번 판단할 때마다, 50%씩 탐색할 후보를 제외할 수 있음. 시간이 단축 됨.
1.5. 이진 탐색 트리(BST)의 장단점
- 장점: 탐색 속도를 개선할 수 있음
- 단점:
- 평균 시간 복잡도는 \(O(\log n)\)이지만, 이는 트리의 양쪽이 모두 균등할 때의 평균 시간복잡도라고 할 수 있음.
- 따라서, 트리가 한쪽으로만 치우쳐져 있는 최악의 경우에는 링크드리스트와 동일한 \(O(n)\)의 성능을 보여줌.
2. 파이썬을 통한 기본적인 이진탐색트리 구현
- 노드와 그 다음 노드를 연결된 형태를 띄기 때문에, 링크드 리스트로 구현하면 용이함.
2.1. 노드 클래스
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
2.2. 최상단에 위치한 head 설정
def __init__(self, head):
self.head = head
2.3. 이진탐색트리에 데이터 저장 (insert)
def insert(self, value):
self.current_node = self.head
# 각 노드를 순회
while True:
if value < self.current_node.value: #현재노드보다 작은 경우 : 왼쪽 가지로 이동
if self.current_node.left != None: # 왼쪽 가지로 이동했을 때, 이미 데이터 노드가 있다면
self.current_node = self.current_node.left # 비교대상 노드를 왼쪽가지 노드로 교체
else: # 데이터 노드가 없다면
self.current_node.left = Node(value) # value를 가지는 새로운 노드를 만들어서 왼쪽 가지에 삽입
break
else: # 오른쪽도 동일함.
if self.current_node.right != None:
self.current_node = self.current_node.right
else:
self.current_node.right = Node(value)
break
2.4. 이진 탐색 트리의 탐색 (search)
def search(self, value):
self.current_node = self.head
# HEAD 노드에서부터 찾고자 하는 노드를 순회하며 찾음
while self.current_node:
if self.current_node.value == value:
return True
elif value < self.current_node.value:
self.current_node = self.current_node.left
else:
self.current_node = self.current_node.right
assert False, "Value does not exist"
2.3. 이진 탐색 트리의 삭제 (delete)
- 노드 삭제의 경우
- 삭제할 노드에 브랜치가 없을 때 : Leat Node 삭제
- 삭제할 노드에 브랜치가 한 개 있을 때 : Childe Node가 하나인 노드 삭제
- 삭제할 노드에 브랜치가 두 개 있을 때 : Childe Node가 둘인 노드 삭제
2.3.1. Case1: Leaf Node 삭제
- 삭제할 Node의 Parent Node가 삭제할 Node를 가리키지 않게 함.
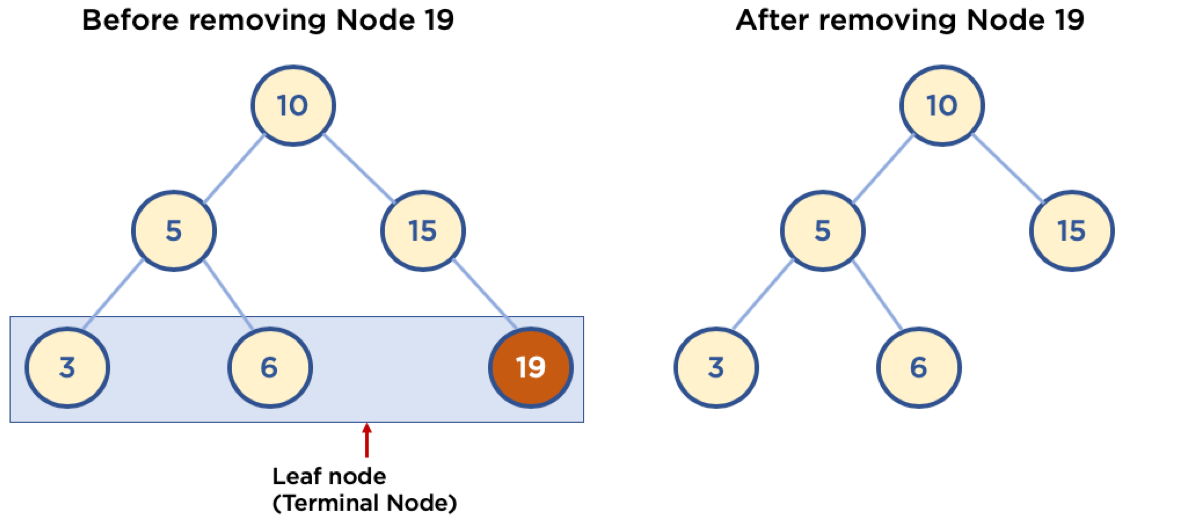
2.3.2. Case2: Childe Node가 하나인 노드 삭제
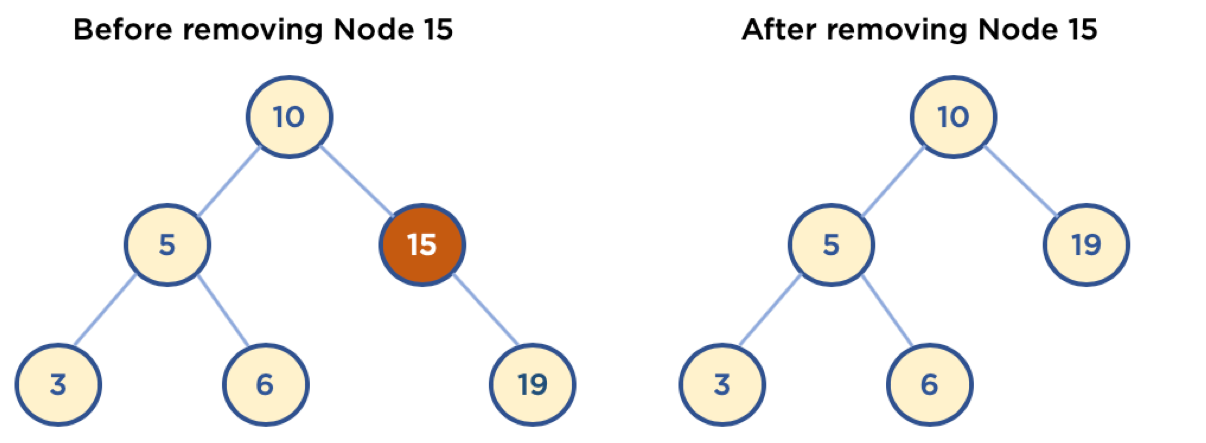
- 삭제할 Node의 Parent Node가 삭제할 Node의 Child Node를 가리키게 함.
2.3.3. Case3: Childe Node가 둘인 노드 삭제
- 구현 방식
- 삭제할 Node의 오른쪽 자식들 중, 가장 작은 값을 삭제할 Node의 Parent Node가 가리키게 함.
- 삭제할 노드의 오른쪽 자식 선택
- 오른쪽 자식의 가장 왼쪽에 있는 노드를 선택
- 해당 노드를 삭제할 노드의 부모 노드의 왼쪽 브랜치가 가리키게 연결
- 해당 노드의 왼쪽 브랜치가 삭제할 노드의 왼쪽 자식 노드를 가리키게 함
- 해당 노드의 오른쪽 브랜치가 삭제할 노드의 오른쪽 자식 노드를 가리키게 함
- 만약 해당 노드가 오른쪽 자식 노드를 가지고 있었을 경우, 해당 노드의 본래 부모 노드의 왼쪽 브랜치가 해당 노드의 오른쪽 자식 노드를 가리키게 함
- 오른쪽 자식의 가장 왼쪽에 있는 노드를 선택
- 삭제할 노드의 오른쪽 자식 선택
- 삭제할 Node의 오른쪽 자식들 중, 가장 작은 값을 삭제할 Node의 Parent Node가 가리키게 함.
Case3-1: 삭제할 노드가 부모 노드의 왼쪽에 있을 때
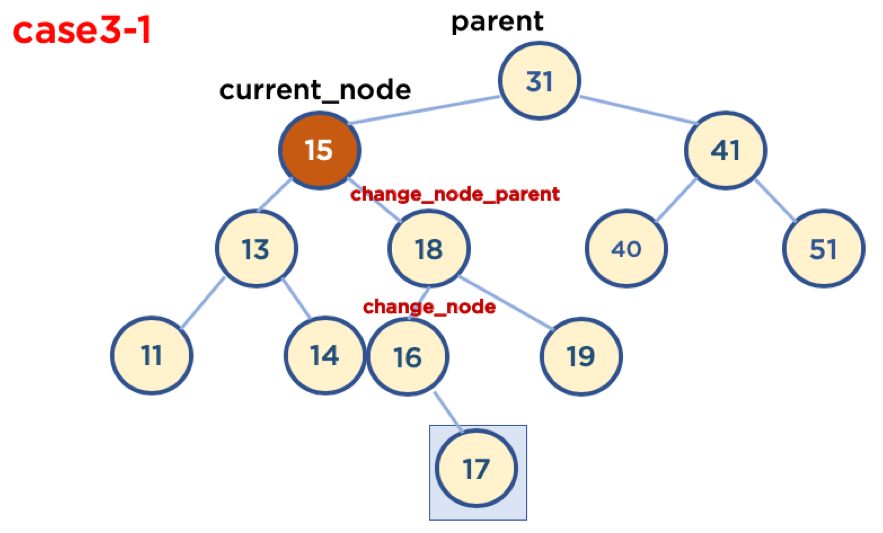
- 삭제할 Node의 오른쪽 자식들 중, 가장 작은 값을 삭제할 Node의 Parent Node가 가리키게 함.
- Case3-1-1: 삭제할 노드가 부모 노드의 왼쪽에 있고, 삭제할 노드의 오른쪽 자식 중 가장 작은 값을 가진 노드의 자식노드가 없을 때.
- Case3-1-2: 삭제할 노드가 부모 노드의 왼쪽에 있고, 삭제할 노드의 오른쪽 자식 중 가장 작은 값을 가진 노드의 오른쪽에 자식 노드가 있을 때
- 노드의 왼쪽으로는 더 작은 값을 가진 노드가 존재하기 때문에, 가장 작은 값을 가진 노드의 자식노드가 왼쪽에 있을 경우는 없음.
Case3-2: 삭제할 노드가 부모 노드의 오른쪽에 있을 때
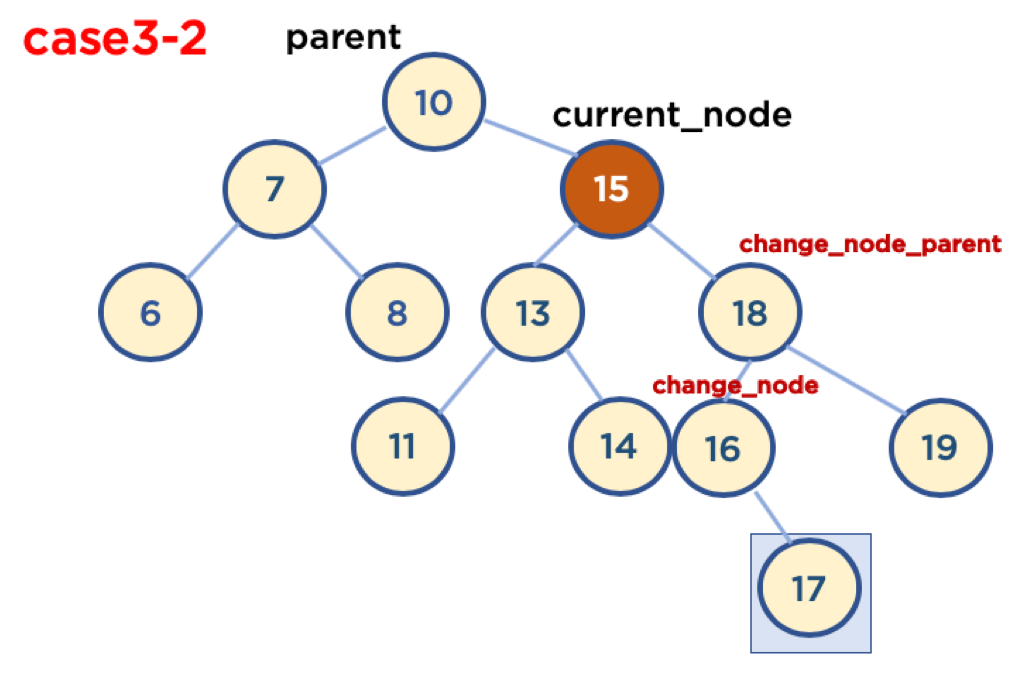
- 삭제할 Node의 오른쪽 자식들 중, 가장 작은 값을 삭제할 Node의 Parent Node가 가리키게 함.
- Case3-2-1: 삭제할 노드가 부모 노드의 오른쪽에 있고, 삭제할 노드의 오른쪽 자식 중, 가장 작은 값을 가진 노드의 자식 노드가 없을 때
- Case3-2-2: 삭제할 노드가 부모 노드의 오른쪽에 있고, 삭제할 노드의 오른쪽 자식 중, 가장 작은 값을 가진 노드의 오른 쪽에 자식 노드가 있을 때.
- 노드의 왼쪽으로는 더 작은 값을 가진 노드가 존재하기 때문에, 가장 작은 값을 가진 노드의 자식노드가 왼쪽에 있을 경우는 없음.
2.3.4. 삭제 코드 구현
def delete(self, value):
searched = False # 삭제할 노드가 있는지 판단하는 boolean
self.current_node = self.head # 현재 노드 선언
self.parent = self.head # 부모 노드 선언
while self.current_node:
if self.current_node.value == value: # 삭제하고자 하는 노드를 찾았다면
searched = True # 삭제할 노드가 있다고 판단함
break
elif value < self.current_node.value:
self.parent = self.current_node
self.current_node = self.current_node.left
else:
self.parent = self.current_node
self.current_node = self.current_node.right
if searched == False:
assert searched, "Node does not exist"
# Case 1
if (self.current_node.left == None) and self.current_node.right == None: # Leaf Node
if value < self.parent.value: # 부모노드의 왼쪽일 경우
self.parent.left = None
else: # 부모노드의 오른쪽일 경우
self.parent.right = None
del self.current_node
# Case 2-1
# 삭제할 노드가 왼쪽에 자식노드 한 개를 가지고 있을 경우
elif (self.current_node.left != None) and self.current_node.right == None:
if value < self.parent.value:
self.parent.left = self.current_node.left
else:
self.parent.right = self.current_node.left
# Case 2-2
# 삭제할 노드가 오른쪽에 자식노드 한 개를 가지고 있을 경우
elif (self.current_node.left == None) and self.current_node.right != None:
if value > self.parent:
self.parent.left = self.current_node.right
else:
self.parent.right = self.current_node.left
# Case 3: 삭제할 노드에 브랜치가 좌우로 존재할 때.
elif (self.current_node.left != None) and self.current_node.right != None:
# Case 3-1:
if value < self.parent_value:
self.change_node = self.current_node.right
self.change_node_parent = self.current_node.right
while self.change_node.left != None:
self.change_node_parent = self.change_node
self.change_node = self.chage_node.left
if self.chage_node.right != None: # Case 3-1-2
self.change_node_parent.left = self.change_node.right
else: # Case 3-1-1
self.change_node_parent.left = None
# 삭제 대상 노드의 부모/자식 노드 간 연결을 끊고, change_node로 대체함.
self.parent.left = self.change_node
self.change_node.right = self.current_node.right
self.change_node.left = self.current_node.elft
# Case 3-2:
else: #value > self.parent_value
self.change_node = self.current_node.right
self.change_node_parent = self.current_node.right
while self.change_node.left != None:
self.change_node_parent = self.change_node
self.change_node = self.change_node.left
if self.change_node.right != None: # Case 3-2-2
self.change_node_parent.left = self.change_node_parent.right
else: # Case 3-2-1
self.change_node_parent.left = None
# 삭제 대상 노드의 부모/자식 노드 간 연결을 끊고, change_node로 대체함.
self.parent.right = self.change_node
self.change_node.left = self.current_node.left
self.change_node.right = self.current_node.right
2.4. 전체 코드
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
class NodeManagement:
def __init__(self, head):
self.head = head
def insert(self, value):
self.current_node = self.head
while True:
if value < self.current_node.value:
if self.current_node.left != None:
self.current_node = self.current_node.left
else:
self.current_node.left = Node(value)
break
else:
if self.current_node.right != None:
self.current_node = self.current_node.right
else:
self.current_node.right = Node(value)
break
def search(self, value):
self.current_node = self.head
while self.current_node:
if self.current_node.value == value:
return True
elif value < self.current_node.value:
self.current_node = self.current_node.left
else:
self.current_node = self.current_node.right
assert False, "Number does not exist."
def delete(self, value):
searched = False
self.current_node = self.head
self.parent = self.head
while self.current_node:
if self.current_node.value == value:
searched = True
break
elif value < self.current_node.value:
self.parent = self.current_node
self.current_node = self.current_node.left
else:
self.parent = self.current_node
self.current_node = self.current_node.right
if searched == False:
assert False, "Number does not exist."
if (self.current_node.left == None) and self.current_node.right == None:
if value < self.parent.value:
self.parent.left = None
else:
self.parent.right = None
elif (self.current_node.left != None) and self.current_node.right == None:
if value < self.parent.value:
self.parent.left = self.current_node.left
else:
self.parent.right = self.current_node.left
elif (self.current_node.left == None) and self.current_node.right != None:
if value > self.parent.value:
self.parent.left = self.current_node.right
else:
self.parent.right = self.current_node.left
elif (self.current_node.left != None) and self.current_node.right != None:
if value < self.parent.value:
self.change_node = self.current_node.right
self.change_node_parent = self.current_node.right
while self.change_node.left != None:
self.change_node_parent = self.change_node
self.change_node = self.chage_node.left
if self.chage_node.right != None:
self.change_node_parent.left = self.change_node.right
else:
self.change_node_parent.left = None
self.parent.left = self.change_node
self.change_node.right = self.current_node.right
self.change_node.left = self.current_node.elft
else:
self.change_node = self.current_node.right
self.change_node_parent = self.current_node.right
while self.change_node.left != None:
self.change_node_parent = self.change_node
self.change_node = self.change_node.left
if self.change_node.right != None:
self.change_node_parent.left = self.change_node_parent.right
else:
self.change_node_parent.left = None
self.parent.right = self.change_node
self.change_node.left = self.current_node.left
self.change_node.right = self.current_node.right
return True
데이터 입력
import random
nums = set()
while len(nums) != 100:
nums.add(random.randint(0, 999))
print(nums)
{512, 518, 525, 526, 536, 25, 539, 551, 53, 57, 570, 61, 62, 576, 577, 592, 597, 87, 600, 90, 602, 619, 110, 112, 113, 124, 130, 643, 133, 654, 143, 663, 154, 670, 160, 690, 188, 204, 209, 723, 212, 226, 232, 747, 748, 237, 754, 759, 248, 251, 259, 262, 775, 774, 272, 273, 274, 275, 277, 278, 791, 796, 798, 809, 815, 307, 829, 325, 332, 333, 847, 851, 852, 853, 355, 358, 888, 376, 894, 909, 400, 913, 912, 409, 929, 930, 422, 936, 425, 426, 446, 458, 466, 986, 477, 996, 488, 495, 499, 500}
head = Node(500)
bst = NodeManagement(head)
for num in nums:
bst.insert(num)
데이터 탐색
# 탐색 대상 노드가 존재하는 경우
bst.search(643)
True
# 탐색 대상 노드가 존재하지 않는 경우
bst.search(879)
---------------------------------------------------------------------------
AssertionError Traceback (most recent call last)
<ipython-input-10-03b987c0a6aa> in <module>
----> 1 bst.search(879)
<ipython-input-6-bbcc66356cab> in search(self, value)
39 self.current_node = self.current_node.right
40
---> 41 assert False, "Number does not exist."
42
43
AssertionError: Number does not exist.
데이터 삭제
# 숫자 10개 랜덤 선택
target_nums = set()
while len(target_nums) != 10:
target_nums.add(list(nums)[random.randint(0, 99)])
print(target_nums)
{160, 325, 518, 332, 525, 912, 62, 57, 602, 25}
for delete_num in target_nums:
bst.delete(delete_num)